小惑星は、太陽系空間の中を運動しています。その運動は、基本的には太陽を焦 点とした楕円軌道になっています。そんなことは当たり前だ、とおっしゃる方も多 いでしょうし、学校でならったような「ケプラーの法則」などあまり思い出したく ない、という方もいらっしゃると思います。それに、きちんと天体の運動を計算するためには、「摂動論」という難しい理 論をもちださなければなりませんし。。。

　ご安心下さい。ここでは、ちょっと別の見方で、小惑星の運動に迫ってみようと 思います。ここでいう「別の見方」というのは、時間と空間を超越した（？）よう なものです。ご用とお急ぎでない方は、しばらくお付き合い下さい。

　以前のこの講座（「あすてろいど」NO.92-03、NO.93-03）で、「共鳴（レゾナン ス）」ということにつてお話したことがあります。これは、単純に言えば、木星が 太陽の周りを１回公転するときに小惑星がちょうど２回公転するような運動のこと です。この場合を、２：１の共鳴と呼びます。たとえば、木星が３公転するときに 小惑星が４公転すれば４：３の共鳴と呼びます。要するに、木星などの惑星と小惑 星の公転周期の比が簡単な整数倍になるときを「共鳴」と呼ぶわけです。

　さて、この共鳴について「時間と空間を超えて見る」と、面白いことに出会うこ とができます。図１を見てください。これは、木星と３：１の共鳴にある小惑星の 運動です。どうですか？　太陽系空間に巨大な「花」が咲いたように見えません か？

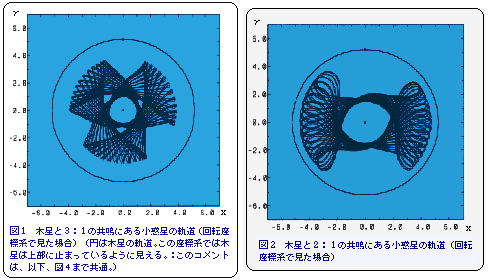
　ここで、再度、図1が普通の見方で見たものではないことに注意してください。 「普通の見方」で見れば、木星も小惑星もただ太陽の周りを楕円軌道を描いて運動 しているだけです。では、どうしてこの「花模様」が出現したのでしょうか？　種 明かしをすると、ここでは、木星が止まってみえるような立場で見ているためなのです。難しい言葉で言えば、「木星の公転運動と同じ角速度で運動する回転系に座標変換して見た」ためです。（この図では、木星は図中の一番上のところで止まって見えます。）

　では、別の共鳴についても見てみましょう。図２は木星と２：１の共鳴です。こ れは何に見えるでしょうか？　大きなリボンのようにでも見えますか？

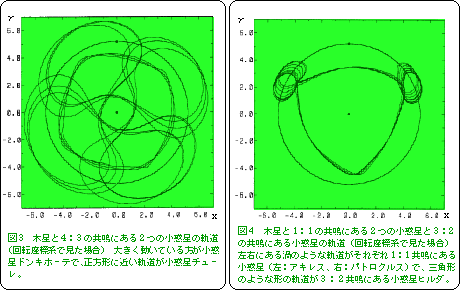
　さらに、図3には、木星と４：３の共鳴にある場合です。ここでは、木星軌道以外 に２つの小惑星の軌道を描いています。特に派手に動いている方は、その名も 「ドンキホーテ」と呼ばれる小惑星の運動です。ドンキホーテらしく（？）非常に 特殊な軌道でさ迷っているようですね。図3のように、普通に紙に印刷してしまうと わかりにくいのですが、このドンキホーテの軌道を立体的に見ると、まさに太陽系 に咲いた大輪の花のようになっています。もう１つのおとなしい動きをしている方 はチューレという名前の小惑星ですが、これも４：３の共鳴にあります。この場合 には、軌道は膨れた正方形のように見えますね。これらの４：３共鳴にある小惑星 をチューレ群と呼んでいます。

　ついでに、１：１共鳴や３：２共鳴について図4に示します。この図では３つの小 惑星の軌道が描かれています。まず、左右で小さな渦を描くように動いているのが トロヤ群と呼ばれる小惑星の群に属する２つの小惑星の軌道で、これが１：１共鳴 です。１：１共鳴というのは、木星と同じ周期で動いている訳ですから、このよう に木星から一定のところで運動しています。また、膨らんだ三角形の軌道を描いて いる方が３：２の共鳴にある小惑星です。この３：２の共鳴にある小惑星をヒルダ 群と呼んでいます。

　このように、いろいろ面白い軌道が見られるのも、座標変換によって見る立場を 変え、さらに小惑星の運動を何周期分も追跡したためです。つまり、この場合は非 常に単純なものではありますが、「時間と空間を超える」ことで、このような面白 い現象に出会うことができたのです。また、これらはいずれも共鳴というものに本 質的に関係しています。共鳴現象は、まじめに扱うと難しい問題ですが、このよう に見るとなんだか楽しい感じになりませんか？　たまには気分を変えて、別の見方 から見るのもいいですね。

（通信総合研究所）

参考： ここで紹介しているものは、「小惑星の分布と運動」（日経サイエンス、1992年10 月号）の記事の内容の一部を書き直してみたものです。元の記事では、ここで示し た軌道を立体的に見ることができますので、機会がありましたら是非ご覧くださ い。